Magneto-rotational instability

In my postdoc at PPPL, Princeton University, I collaborated with Dr. Fatima Ebrahimi and Prof. Eric Blackman to work on systems that are unstable to magneto-rotational instability (MRI).
MRI is required to provide for angular momentum transport in accretion disks at rates consistent with that inferred from observations. Also needed in accretion discs are large-scale magnetic fields for forming jets and nonlocal transport of angular momentum and also for understanding the saturation of MRI.
Using shearing box simulations of MRI, it was shown that even before MRI saturated, a large-scale component of the magnetic fields grows exponentially, basically in the absence of turbulence. The large-scale dynamo was investigated using the mean-field equations and individual contributions to large-scale field growth from EMF and shear terms were identified.

Another interesting result we obtained was the following:
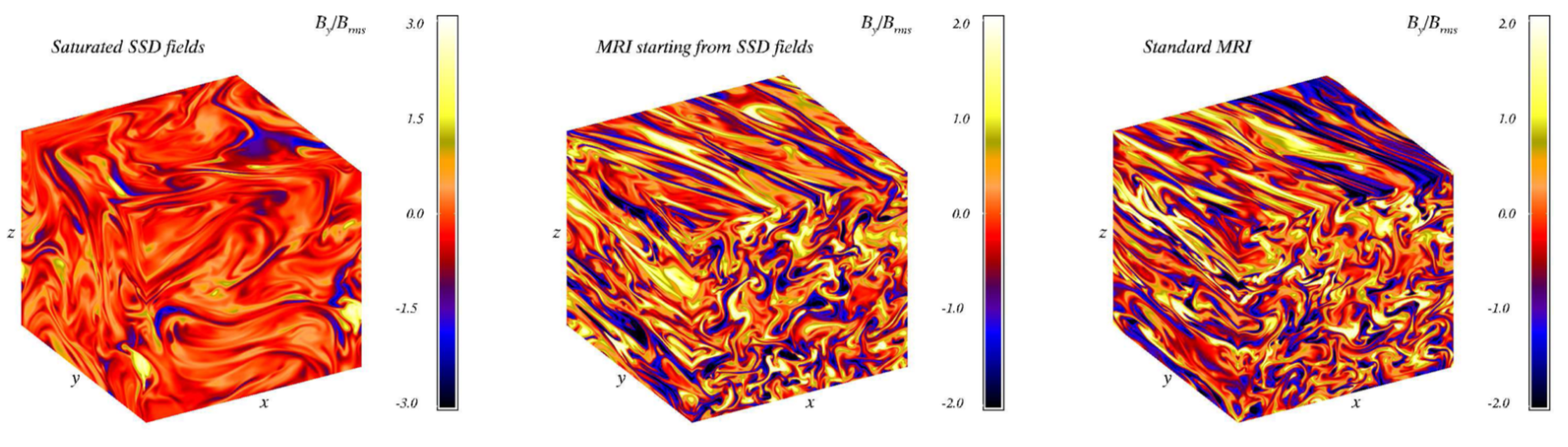
The ubiquitous presence of turbulent or random flows in astrophysical plasmas generically leads to a small-scale dynamo (SSD), which would provide initial seed turbulent velocity and magnetic fields in the plasma that becomes an accretion disc. As a conceptual and practical experiment, I investigated whether the MRI can grow from such small-scale turbulent fields. This is in contrast to previous MRI simulations always where the initial magnetic field included a significant system-scale component, even if stochastic.
In the numerical experiment, I supplied a standard shearing box with isotropically forced SSD generated magnetic and velocity fields as initial conditions, and removed the forcing. It was found that if the initially supplied fields are too weak or too incoherent, they decay from the initial turbulent cascade faster than they can grow via the MRI. When the initially supplied fields are sufficient to allow MRI growth and sustenance, the saturated stresses, large-scale fields, and power spectra match those of the standard zero net flux MRI simulation with an initial large scale vertical field.